merge sort 알고리즘은 배열을 두 개의 부분 배열로 나눈 뒤에, 각각의 배열을 정렬합니다. 그 결과를 바탕으로 정렬하는 알고리즘입니다. 아래와 같은 과정을 거칩니다.
- 두 배열로 나눈다.
- 나눈 배열을 정렬한다.
- 정렬된 두 배열을 합친다. [link]
이 중, 정렬된 두 배열을 합치는 과정은 이 글에서 설명을 했습니다. 위 두 가지 과정을 이 글에서 설명하겠습니다.
작은 문제로 나누기
큰 문제를 해결하는 것은 어렵습니다. 대신, 작은 문제로 쪼개는 것은 쉽습니다. merge sort 알고리즘은 먼저, 큰 문제를 작은 문제로 쪼개는 것부터 시작합니다. 예를 들어, 크기가 4인 배열을 정렬한다고 생각해 봅시다.

큰 문제는 arr의 1번째 원소부터 4번째 원소까지를 오름차순으로 정렬하는 것입니다. 이를 두 부분 문제로 쪼갭니다.
- arr의 1번째 원소부터 2번째 원소까지 정렬
- arr의 3번째 원소부터 4번째 원소까지 정렬
그런데, 이 두 부분 문제도 어려워 보입니다. 또 쪼개 봅시다.
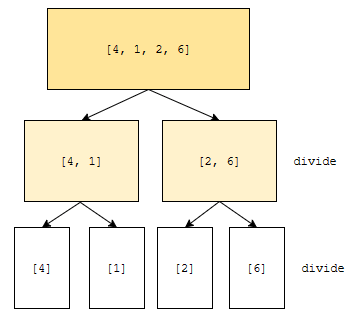
저는 arr의 1번째 원소부터 2번째 원소까지 정렬하는 문제를 아래와 같이 쪼갰습니다.
- arr의 1번째 원소부터 1번째 원소까지 정렬
- arr의 2번째 원소부터 2번째 원소까지 정렬
그리고, arr의 3번째 원소부터 4번째 원소까지 정렬하는 문제를 아래와 같이 쪼갰습니다.
- arr의 3번째 원소부터 3번째 원소까지 정렬
- arr의 4번째 원소부터 4번째 원소까지 정렬
arr의 i번째 원소부터 i번째 원소까지 정렬하는 문제는 쉽습니다. 크기가 1이여서, 정렬할 필요가 없기 때문입니다. 부분문제로 쪼개는 것은 여기서 끝입니다. 여기까지 코드를 볼게요.

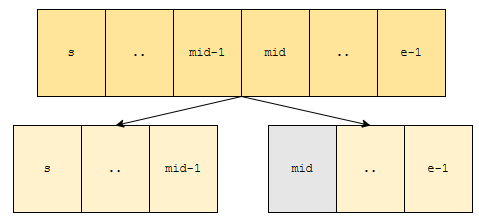
s번째 원소부터 e-1번째 원소까지 배열 tar를 오름차순으로 정렬합니다. 이 문제는 어렵습니다. 나누면 쉽습니다. 이를 어떻게 나누었나요?
- s번째 원소부터 mid-1번째 원소까지 정렬
- mid번째 원소부터 e번째 원소까지 정렬
그런데, 이 함수는 언제 빠져나오나요? s+1이 e보다 크거나 같을 때 빠져나와요. 즉, s번째 원소부터 e-1번째 원소까지 정렬하는데, e가 s+1이라면, s번째 원소부터 s번째 원소까지 정렬하는 것이랑 같기 때문입니다.
여기까지 부분 문제로 쪼갰습니다. 자. 이 상태로 정렬이 되었을까요? 아닙니다. 왜?
- 부분문제로 쪼개기만 했습니다.
- 부분문제를 합치는 과정을 수행하지 않았습니다.
쪼갠 부분문제들을 해결한 후에, 이를 합치는 과정이 필요하겠네요? 정복 과정이 필요한 것입니다.
합칠 때 정복하기
부분 문제를 해결한 결과를 바탕으로, 큰 문제를 해결한다. 정복하는 과정입니다. merge sort 알고리즘에서는 어떨까요?
- 작은 두 배열이 정렬되었어요.
- 그 결과를 바탕으로, 정렬된 두 배열 합치면 되겠군요.
그러면, 합쳐 봅시다.
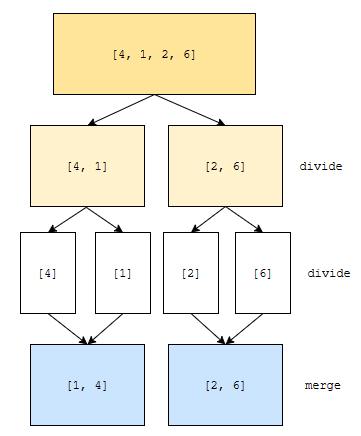
[4, 1]의 부분 배열 [4]와 [1]은 정렬된 상태입니다. 이를 토대로 [4, 1]을 오름차순으로 정렬할 수 있나요? 두 배열에서 작은 순서대로 뽑으면 되기 때문입니다. 그러면 1이 먼저 뽑히고, 그 다음에 4가 뽑히게 됩니다. 즉, 1번째 원소부터 2번째 원소까지 정렬하라는 문제에 대한 결과는 [1, 4]가 됩니다.
다음, [2, 6]의 부분 배열 [2]와 [6]은 정렬된 상태입니다. 이를 토대로 [2, 6]을 오름차순으로 정렬할 수 있어요. 작은 순서대로 뽑으면 2 다음에 6이 뽑히기 때문입니다. 즉, 3번째 원소부터 4번째 원소까지 정렬하라는 문제에 대한 결과는 [2, 6]이 됩니다.
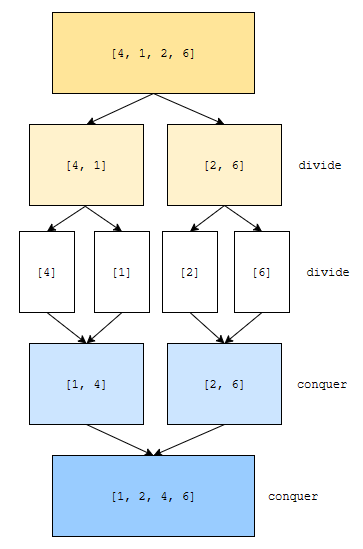
이제 아래 2개의 문제가 해결되었습니다.
- arr의 1번째 원소부터 2번째 원소까지 오름차순으로 정렬
- arr의 3번째 원소부터 4번째 원소까지 오름차순으로 정렬
이를 토대로, arr의 1번째 원소부터 4번째 원소까지 오름차순으로 정렬할 수 있습니다. 이를 조금 더 확장해 볼까요?

아래 부분 문제들이 해결되었습니다.
- s번째 원소부터 mid-1번째 원소까지 오름차순으로 정렬
- mid번째 원소부터 e-1번째 원소까지 오름차순으로 정렬
이 때, s번째 원소부터 e-1번째 원소까지 오름차순으로 정렬하라는 문제를 O(e-s)에 해결할 수 있습니다. merge 코드를 보겠습니다.

s번째 원소부터 mid-1번째 원소까지 정렬되었고, mid번째 원소부터 e-1번째 원소까지 정렬되었어요. 그러면, left는 s부터 mid-1번까지, right는 mid부터 e-1번까지 순회하면 됩니다. 28번째 while loop가 이 역할을 해요.
pos가 처음에 0으로 초기화 되었는데요. 이는, 정렬된 결과를 임시 저장하기 위한 배열의 크기를 e – s + 1로 선언했기 때문이에요. 대강 이런 그림이라고 생각하시면 됩니다.
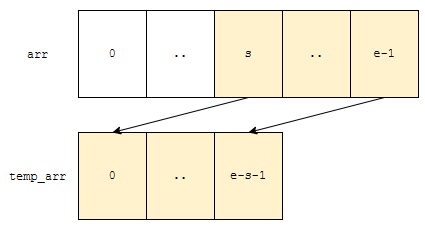
다음에, merge_sort 코드를 봅시다. 이건 크게 어렵지 않습니다.

merge_sort로 부분 문제들을 해결하고, merge 함수로 conquer 하는 형태입니다. 보통, 분할 정복은 위와 같은 구조를 보이게 됩니다. 전체 소스 코드는 이 코드를 보시면 됩니다.