우선순위 큐 자료구조를 이용하는 문제는 코딩 테스트에서 의외로 자주 나오곤 합니다. 저 또한 이 자료구조를 이용해서 풀어야 하는 문제를 많이 출제하곤 했습니다. 제가 출제한 문제들 중, 해당 자료구조를 쓰는 문제들은 아래와 같습니다.
이 자료구조는 아래와 같은 연산을 로그와 같거나 더 좋은 복잡도로 수행할 수 있습니다.
- 가장 우선 순위가 높은 원소 찾기
- 가장 우선 순위가 높은 원소 제거하기
- 원소 추가하기
이번 시간에는 이 자료구조가 어떻게 동작하는지 간략하게 알아봅니다.
pq에 대한 이야기
우선순위 큐. 우선순위가 있어요. 즉, 데이터에 priority가 있다는 것이 포인트입니다. 그래서, priority가 높은 것이 먼저 빠지는 특성이 있어요. 그리고 완전 이진트리 구조를 가져요. 질문. 여기서 우선순위는 어떻게 정의될까요? 사실, 정의하기 나름입니다.
- 제일 큰 것
- 제일 작은 것
전자는 max heap, 후자는 min heap이라고 합니다. 이들은 어떻게 저장되는가?
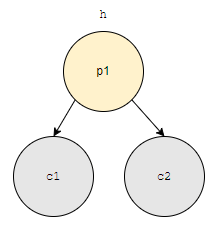
부모 노드가 자식 노드들보다 우선 순위가 높습니다. 위 그림에서 c1, c2의 부모는 p1입니다.
- p1이 c1보다 우선순위가 높거나 같습니다.
- p1이 c2보다 우선순위가 높거나 같습니다.
이 구조를 유지한다면, 우선 순위가 제일 높은 데이터는 root가 됩니다. 이제 각각의 노드들을 번호로 표시해 보겠습니다. 이 트리에 p1, c1, c2, g1, g2 순으로 추가되었다고 해 보겠습니다. c1은 g1, g2보다 우선순위가 높거나 같다고 하면, 아래와 같이 추가되어 있을 겁니다.

그러면 아래와 같이 정리를 할 수 있습니다.
- 루트 노드는 1번입니다.
- 루트 노드의 자식 2개는 2번, 3번입니다.
- 2번 노드의 자식 2개는 4번, 5번입니다.
이를 일반화 시키면 아래와 같습니다.
- x번 노드의 부모 노드는 [x/2]번 노드입니다. 단, 1번 노드의 부모 노드는 없습니다.
- x번 노드의 자식 노드는 2x, 2x+1번 노드입니다.
완전 이진 트리이니, n개의 원소가 추가되었다면, n번 노드까지 원소가 있습니다.
원소 추가하기
Min heap h가 아래와 같이 있습니다.
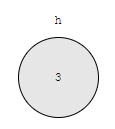
3이 하나 저장되어 있군요. 2를 추가해 보겠습니다.
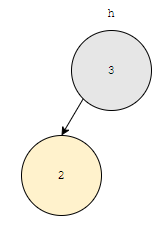
그러면, 위 그림과 같이 됩니다. 여기서 2가 적혀진 노드의 부모는 3이 적혀진 노드입니다. Min heap에서 2가 3보다 우선순위가 높습니다. 그런데, 부모보다 자식의 우선순위가 더 높은 상황이 발생했어요. 이 경우, 부모와 자식을 바꿉니다.
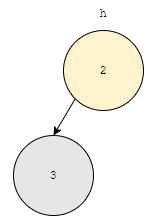
root가 2이고, 2의 자식은 3입니다. 루트의 자식은 루트보다 우선순위가 낮거나 같네요. 고로, heap의 조건을 만족합니다. 여기서 break 합니다.
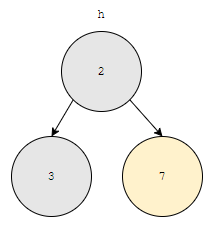
이제 7을 추가합니다. 7의 부모는 2입니다. 2가 7보다는 Min heap에서 우선 순위가 높아요. 우선순위 큐의 조건을 만족하기 때문에 break 합니다.

다음에 2를 추가해 보겠습니다. 노란색 노드의 부모 노드에는 3이 적혀져 있어요. 문제는, 부모 노드보다 자식 노드의 우선 순위가 더 높습니다. 따라서, 부모와 자식의 값을 바꿉니다.

그리고, 4번 노드의 부모인 2번 노드로 올라갑니다. 이제 이 (노란색으로 표시한) 노드와 (파란색으로 표시한) 부모 노드를 비교합니다. 2와 2의 우선 순위는 같네요? 따라서, 여기서 break를 겁니다. 여기까지 로직을 정리해 봅시다.
- n개의 원소가 있는 우선순위 큐에 원소 x가 추가되었습니다.
- n+1번 노드에 x를 추가합니다. 현재 보고 있는 위치는 n+1번입니다.
- 해당 노드의 부모 노드의 우선 순위가 더 낮으면
- 부모와 자식의 값을 바꿉니다.
- 현재 보고 있는 위치를 부모 노드로 바꿉니다.
- 그렇지 않으면 빠져 나옵니다.
- 해당 노드의 부모 노드의 우선 순위가 더 낮으면
- n+1번 노드에 x를 추가합니다. 현재 보고 있는 위치는 n+1번입니다.
여기까지 이해가 되셨다면, 가장 우선순위가 높은 원소를 제거하는 연산을 이해해 봅시다.
우선순위가 높은 원소 제거하기
우선 순위가 높은 원소를 제거하면, 일시적으로 pq의 조건을 만족하지 않게 됩니다. 이 때에는 어떻게 할까요? 제거하기 전에 원소가 n+1개 있었다면, n+1번 노드에 있는 값을 root로 올립니다. 이 과정을 보도록 합시다.
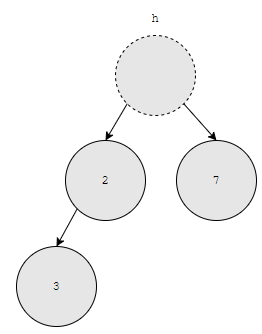
priority가 가장 높은 2를 제거했습니다. 이 경우, pq의 조건을 만족하지 않습니다. 고로, 4번 노드에 있는 3을 맨 위로 올립니다.

이제, 우선순위 큐 조건을 만족하는지 봐야 합니다. 현재 보고 있는 노드는 root입니다.
- root의 자식들 중 우선순위가 높은 것을 찾습니다.
- 2와 7 중에 Min heap에서 priority가 높은 것은 2입니다. 따라서 root와 2를 비교합니다.
- 부모인 3보다, 자식인 2의 우선 순위가 더 높기 때문에, 부모와 자식의 값을 바꿉니다.
부모와 자식의 값을 바꾸면 어떻게 될까요?
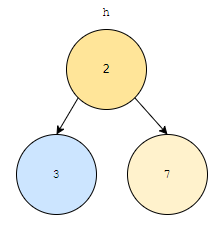
위 그림과 같이 됩니다. 그러면, 최소한 root와 루트의 자식들은 pq의 조건을 만족합니다. 2는 3과 7보다 우선 순위가 더 높거나 같기 때문입니다. 이제, 군청색으로 표시한 3과 자식들을 비교해야 하는데요. 비교할 자식들이 없네요? 알고리즘을 종료합니다.
조금 더 복잡한 예제를 봅시다.
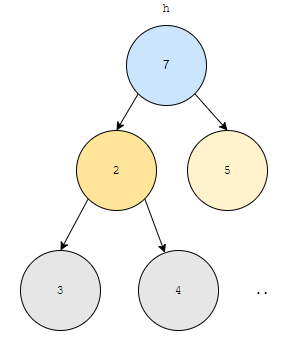
6번 노드를 root로 올린 직후입니다. 이 경우도 Min heap을 만족하지 않아요. 루트부터 시작합니다. 루트 노드의 자식 노드 2번과 3번 노드 중, 우선 순위가 높은 것은 2번 노드입니다. 그렇기 때문에 2번을 선택합니다. 7과 2를 비교하니까, 자식이 더 높네요?
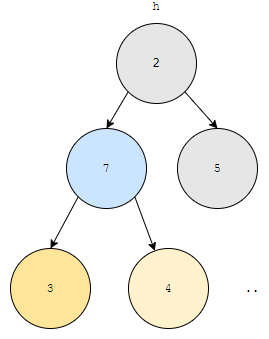
고로, 1번과 2번 노드의 값을 바꿉니다. 그리고, 현재 보고 있는 노드를 2번으로 바꿉니다. 이 노드의 자식은 4번과 5번 노드입니다. 4번 노드에는 3, 5번 노드에는 4가 적혀져 있으니, Min heap 에서는 4번 노드가 더 높네요?
그렇다면 이 노드와 2번 노드의 우선 순위를 비교해야 할 건데, 3이 7보다 우선 순위가 높아요. 자식 노드가 더 높으니, 부모와 자식을 바꿉니다.
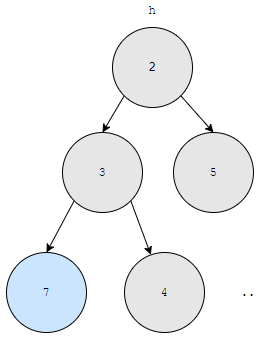
보고 있는 현재 노드는 4번이 됩니다. 이 노드의 자식은 없으니 빠져 나옵니다. 이제, 여기까지 로직을 정리해 봅시다.
- 우선순위가 높은 원소를 삭제하기 전에 n + 1개의 원소가 있었습니다. 삭제 후
- n + 1번 노드에 있었던 원소를 1번 노드에 올립니다. root 위치로 갑니다.
- 현재 보고 있는 노드는 1번 노드입니다.
- 현재 보고 있는 노드의 자식 노드들 중 우선 순위가 높은 자식 노드 c를 가져 옵니다. – #
- 자식 노드 c보다 현재 보고 있는 노드의 우선 순위가 높으면 break
- 그렇지 않으면
- 부모와 자식의 값을 바꿉니다.
- 현재 보고 있는 노드를 자식노드 c의 위치로 바꾸고 #을 다시 반복합니다.
이렇게 해서 우선순위 큐의 조건을 유지시킵니다. 크기가 n이라면, depth는 log scale입니다. 그리고, 추가던 제거던 한 번 사이클 돌 때 마다 뎁스가 하나씩 변하므로, 복잡도는 log scale이 됩니다.