안녕하세요. memcpy, memmove를 배웠으니, 이를 활용할 수 있는 삽입 정렬 (insertion sort) 알고리즘에 대해 알아보도록 하겠습니다. 아래 글을 보고 오시면 조금 더 이해하기 수월하실 거에요.
어떻게 동작하는가?
먼저 삽입 정렬의 동작 방식을 간단하게 알아보겠습니다.

먼저, 아직 위치에 들어가지 않은 x가 있습니다. x 앞에는 sorted data, 즉 이미 정렬된 것들이 있습니다. 우리는 이 보라색 안에, x를 넣어야 합니다. 그런데, 보라색 부분에는
- x보다 작거나 같은 원소
- x보다 큰 원소
이렇게 두 부분으로 나누어져 있을 겁니다.

당연하게도, 정렬이 되어 있다면 x보다 작거나 같은 것이 먼저 나오고, 그 후에 x보다 큰 것이 나올 겁니다. x는 어디에 넣으면 될까요?
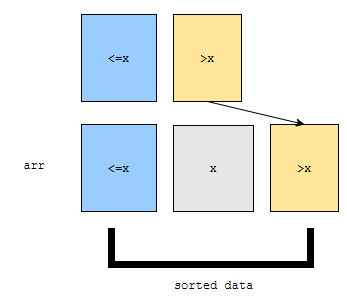
노란색 앞에 넣으면 되겠지요? 그러면, x보다 작거나 같은 원소, x, 그리고 x보다 큰 것 순서대로 나옵니다. 또한, 군청색과 노란색은 정렬되었기 때문에, 제가 표시한 구간도 정렬되어 있습니다. 1 사이클이 돌 때 마다 이 작업을 반복하면 되는 것이지요.
예제를 보겠습니다. 4, 2, 3, 5 순서대로 저장되어 있는 배열을, 오름차순으로 정렬해야 한다고 하겠습니다.
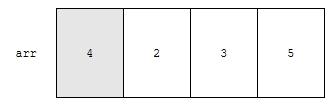
처음에 4를 넣습니다. 4 앞에 이미 정렬된 데이터가 없습니다. 그러니, 그대로 둡니다.

다음에 2를 넣어야 합니다. 그런데, 앞에 이미 정렬된 부분에서 2보다 작은 부분은 없어요. 2보다 큰 것만 있는 상황이지요. 따라서, 노란색 부분을 뒤로 1칸 밀어버리고, 2를 0번째 위치에 넣습니다.
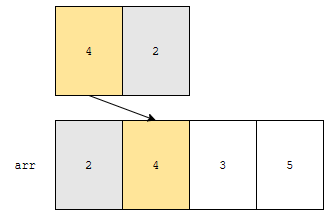
2회전이 끝나면, 2, 4, 3, 5 순서대로 되게 됩니다. 이미, 0 ~ 1번째 원소는 sort가 되어 버립니다.
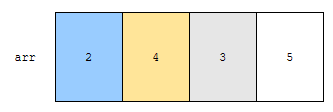
다음에, 3을 넣어야 해요. 그런데 3보다 작거나 같은 것은 앞에 1개 있어요. 뒤에 노란색 부분은 3보다 큽니다. 따라서, 3이 들어가야 할 위치는 1번째 위치입니다. 1번째 위치에 3을 넣고, 노란색 부분을 뒤로 1칸 밀어버립니다.

3회전까지 끝나면, 2, 3, 4, 5 순으로 sort가 됩니다.

다음 5를 넣습니다. 그런데, 5보다 큰 것은 없어요. 작거나 같은 것만 이미 sorted 된 구간에 있는 상황입니다. 따라서, 아무 것도 하지 않습니다. 정렬이 완료되었습니다.
삽입 정렬 코드 보기
이제, 간단하게 코드를 보겠습니다.
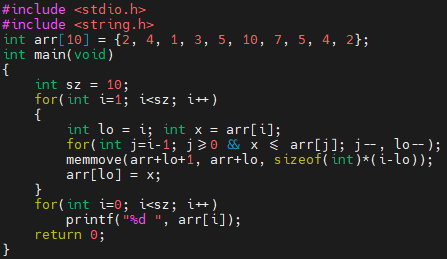
arr을 정렬합니다. 맨 처음에는 insertion 연산이 일어나지 않으니 i=1부터 돌게 됩니다. 매번 돌 때마다 중요하게 다루어지는 변수는 아래 3개입니다.
- i
- x
- lo
여기서 x는 넣어야 하는 값을 의미합니다. i와 lo가 어떤 값인지 따라가 보도록 할게요.

먼저 lo와 i는 3입니다. 즉, 4번째 원소인 5를 가리킵니다. j는 3번째 원소 바로 전인 2번째 원소를 가리킬 겁니다.
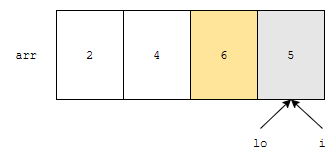
5보다는 6이 큽니다. 따라서, lo는 하나 감소합니다. 그리고, 4를 보게 될 겁니다.

4는 5보다 작거나 같습니다. 따라서 lo는 2가 됩니다. i-lo는 1이 되는데, 이는 옮겨야 할 원소의 개수를 의미합니다. lo번째 위치에 5를 추가해야 하는 상황이므로, src는 arr + lo가 되고, dest는 arr + lo + 1이 됩니다.

결과는 위와 같습니다. 시간 복잡도는 어떻게 될까요? 위치를 탐색하는 데 최악의 경우, n만큼 걸리고, 이를 n번 반복하므로, 복잡도는 O(n2)가 됩니다. 추가할 위치를 탐색하는 복잡도를 이진 탐색을 이용하여 O(log2n)으로 낮출 수 있습니다만, 최악의 경우 1사이클 당 n회 복사하기 때문에, 복잡도는 O(n2)가 됩니다. 다만, 정렬이 작은 데이터에 대해서, 정말 빨리1 수행되기 때문에, 하이브리드 sort에서 기저 조건에서 많이 쓰이는 편입니다.
이진 탐색을 이용해서, insertion할 위치를 찾는 복잡도를 낮추는 것은 과제로 드리겠습니다.
- 심지어 메모리 복사 함수로 최적화 할 여지도 꽤 있기 때문에 ↩︎