이 글에서는 이진 탐색 (binary search)과 시간 복잡도를 알아보도록 하겠습니다. 절반씩 후보해를 줄이는 것이나, 이진법에 기반한 아이디어는 의외로 많이 쓰이니 알아두시면 좋습니다.
어떤 알고리즘인가?
이진 탐색이 어떤 아이디어를 기반으로 작동하는지 간단하게 설명해 볼게요. 오름차순으로 정렬된 배열에서 x를 찾으려고 합니다.
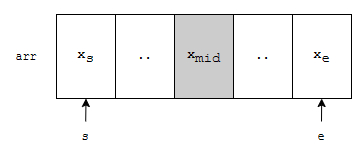
그러면 배열의 시작 부분과 끝 부분과 중간 부분이 있을 겁니다. 중간 부분을 편하게 xmid 라고 합시다. 이 수가 x와 같으면 당연하게도 탐색이 끝났을 겁니다. 그런데, 이런 경우도 있어요.
- x가 xmid 보다 작은 경우
- x가 xmid 보다 큰 경우
전자의 경우, mid 보다 왼쪽에서, 후자의 경우 오른쪽 부분에서 찾는 것이 이진 탐색의 핵심이라고 할 수 있어요.
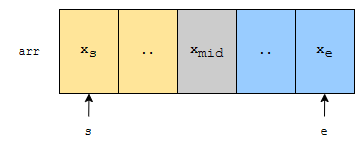
즉, 찾으려는 수 x가 xmid보다 작은 경우, 노란색 부분에서 탐색을 계속하고, xmid보다 크다면, 군청색 부분에서 탐색합니다. 이게 기본 아이디어입니다. 왜 이렇게 해도 될까요? 먼저, xmid보다 큰 수가 노란색 부분에서 나온다고 해 봅시다. 이 경우
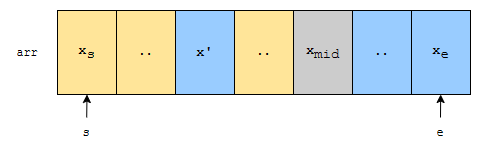
위와 같이 상황이 그려집니다. 노란색 영역에 뜬금없이 xmid보다 큰 수가 나왔기 때문에, 오름차순으로 정렬되어 있다는 전제가 깨져버립니다. 만약에 전제가 깨지지 않으려면, 보라색으로 표시한 부분이 xmid보다 크거나 같은 수가 나와야 합니다.
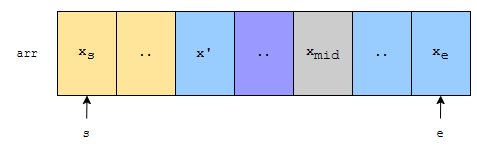
결론적으로 xmid 바로 전에 있는 원소도 x’보다 같거나 클 건데요. 중앙에 있는 것은 xmid 입니다. x’은 xmid보다 큽니다. 따라서, x’보다 크거나 같은 것 역시 xmid보다 큽니다. 전제가 깨져버리는 상황입니다. 따라서, 오름차순으로 정렬이 되어 있다면, xmid 보다 왼쪽에 있는 영역에는 xmid 보다 작거나 같은 수만 나오게 됩니다.
xmid보다 오른쪽에 있는 경우, xmid보다 크거나 같은 수들만 나오는 경우도 사실일까요? 만약에 특정 위치에, 작은 수 s’가 하나 나왔다고 해 보겠습니다.
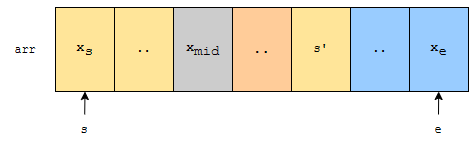
그러면 오름차순 조건을 만족하는 경우, s’보다 왼쪽에 있는 주황색 부분은 s’보다 작거나 같은 수들이 나오게 됩니다. 그러면 xmid 바로 오른쪽에 있는 원소 또한 s’보다 작거나 같아야 합니다. 그런데 s’이 xmid보다 작아요. 그렇기 때문에 xmid의 오른쪽에 xmid보다 작은 원소가 오는 경우, 전제가 깨지게 되어 버립니다.
따라서, 오름차순으로 정렬이 된 경우 아래와 같이 탐색하면 됩니다.
- 찾으려는 수가 중앙에 있는 값보다 작으면 mid의 왼쪽에서
- 중앙에 있는 값보다 크면 mid의 오른쪽에서 탐색
같다면, 바로 해당 위치를 돌려주면 되겠습니다. 이것이 이진 탐색 알고리즘입니다. 당연하게도 정렬이 되어 있지 않으면 동작하지 않습니다. 즉, 이진 탐색 알고리즘의 선결 조건은 정렬입니다.
코드로 구현해 보기
이것을 어떻게 코드로 구현할까요?
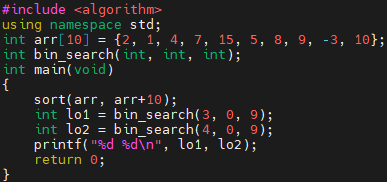
먼저, 정렬된 배열이 필요합니다. sort 함수로 정렬해 주었습니다. 그 다음에 bin_search를 호출해 주었는데요. 찾을 값과 찾을 범위의 시작과 끝 이렇게 3개의 인자를 받습니다.
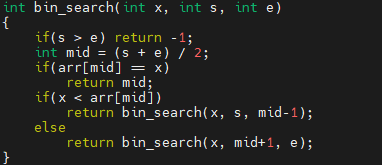
다음, bin_search 함수 내부를 봅시다. s가 e보다 큰 경우 -1을 돌려줍니다. 그렇지 않으면, 중앙값 하나를 얻어와요. 그 다음 3가지 케이스에 대해 처리를 하는데요.
- 중앙값이 찾으려는 값인 경우 mid를 돌려줍니다.
- 중앙값보다 찾으려는 값이 작으면, 탐색 범위를 mid의 좌측으로 줄입니다.
- 그 반대라면, 탐색 범위를 mid의 우측으로 줄입니다.
이게 다입니다. 이 함수가 수행되는 과정을 보겠습니다.
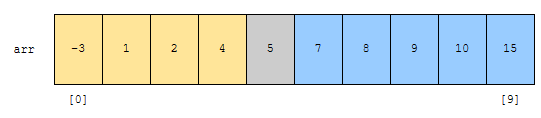
먼저, s가 0, e가 9이고 찾으려는 값이 4라고 해 보겠습니다. 이 경우 mid 값이 4가 됩니다. arr[mid]의 값은 5네요. 찾으려는 값 4가 5보다는 작습니다. 그러면 어떻게 해야 할까요? 왼쪽 범위로 탐색 범위를 좁혀야 겠지요.
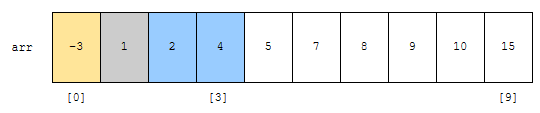
s가 0, e가 3입니다. mid는 1입니다. arr[mid]의 값은 1인데요. 찾으려는 값 4보다는 작습니다. 따라서, 이 경우, 군청색 부분으로 탐색 부분을 좁혀야 합니다.
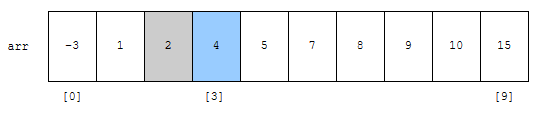
s가 2이고, e가 3입니다. mid는 2입니다. arr[mid]의 값은 2인데요. 이 값보다 4가 더 큽니다. 따라서, 탐색 범위는 군청색 부분이 됩니다.
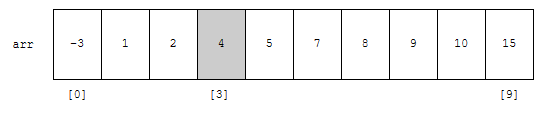
다음, s가 3이고 e가 3입니다. arr[mid]의 값은 4인데요. 제가 찾으려는 값 4와 같습니다. 따라서, 찾은 위치 3을 돌려줍니다.

실행 결과를 볼까요? 2번째 4의 경우 3이 출력됩니다. 1번째 3은 찾을 수 없었으니, -1이 출력됩니다.
시간 복잡도
그러면 이진 탐색 알고리즘의 시간 복잡도는 어떻게 될까요?
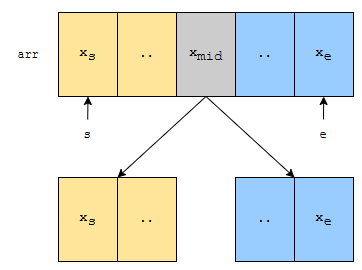
1번 탐색하고 난 후, 탐색 범위가 절반이 되어버립니다. 이것을 언제까지 수행하나요? 탐색 크기가 1이 될 때까지 합니다. 이 말인 즉슨, 크기가 2n인 범위에 대해서, n번 절반으로 쪼개면, 탐색 크기가 1이 된다는 말이 됩니다.
이 정도 케이스로 줄이려면, log 스케일밖에 없습니다. 즉, 크기가 n인 정렬된 배열에 대해서, 이진 탐색의 복잡도는 O(log2n)이 됩니다.