배열 시리즈 중 3번째 글입니다.
- 배열에 대해 알아봅시다. 링크
- row major와 column major에 대해 알아봅시다. 링크
- [현재 글] 배열 주요 연산의 시간 복잡도를 알아봅시다.
- dynamic array에 대해 알아봅시다. 링크
이 글에서는 배열 자료구조의 추가, 삭제, 찾기 연산의 복잡도를 알아봅시다.
먼저 배열 추가 복잡도를 알아봅시다. 원소 개수가 n인 배열이 있다고 해 보겠습니다.
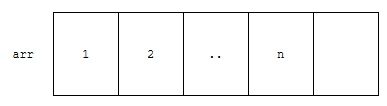
맨 앞, 1번째 위치에 0을 추가해 보겠습니다.
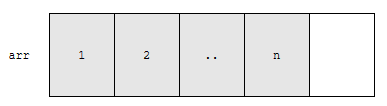
그러면 회색으로 칠한 원소들을 1칸씩 뒤로 밀어야 할 겁니다. 뒤로 밀어야 하는 원소 개수는 배열에 들어 있는 원소의 개수 n과 같습니다.
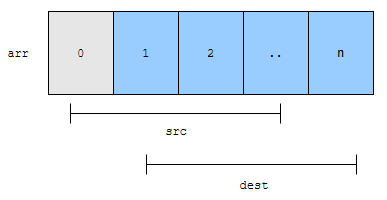
이 원소들을 뒤로 1칸씩 밀어버립니다. 그리고 0번째 위치에 0을 넣으면 됩니다. 이를 일반화 시켜 볼까요? k번째 위치에 0을 넣어보겠습니다. 배열에 있는 원소의 개수는 n입니다.
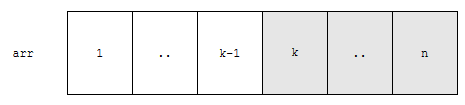
뒤로 밀어야 하는 원소는 회색으로 표시하였습니다. n-k+1인가요? 대충 n-k와 비슷하다고 보시면 됩니다.
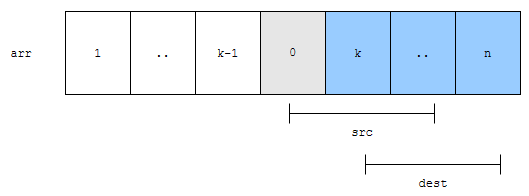
k부터 n까지를 모두 뒤로 민 다음에 k번째 위치에 0을 추가하면 됩니다. 여기까지 정리해 볼까요? 길이가 n인 배열에서 특정 위치에 원소를 추가한다고 해 보겠습니다. 이 때
- 맨 앞에 추가하면 n개의 원소를 뒤로 밀어야 합니다.
- 대신 맨 뒤에 추가하면 어떠한 원소도 뒤로 밀 필요가 없겠지요.
- c++ vector의 push_back, python list의 append 등의 복잡도가 O(1)인 이유입니다.
길이가 n인 배열이 있어요. k번째 위치에 있는 원소를 제거하는 복잡도는 어떻게 될까요?

노란색 부분을 제거해 봅시다. 노란색 부분을 제거한다면, 노란색 부분 뒤에 있는 것들을 앞으로 1칸 당겨와야 합니다. 개수가 어떻게 되나요? n-k가 됩니다.

즉, 우리는 회색 부분을 앞으로 밀어야 한단 말이지요.
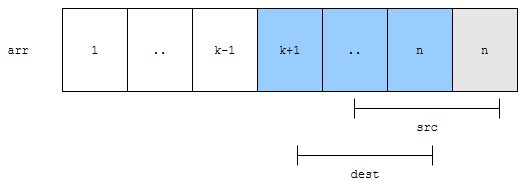
앞으로 밀어 봅시다. 군청색 부분만 유효한 데이터이고, 뒤에 있는 n은 그렇지 않겠네요. 요래 처리하면 됩니다. n-k개가 앞으로 당겨졌다는 의미는 무엇일까요?
- 맨 앞의 원소가 삭제되었을 때 n개를 앞으로 당겨야 합니다.
- 맨 뒤의 원소가 삭제되면 n-n개가 앞으로 당겨집니다.
고로, 배열 삭제 시간복잡도 역시 앞의 것을 삭제하면 O(n), 맨 뒤의 것을 삭제하면 O(1)임을 알 수 있어요. 여기까지 정리하면, 배열에서 insert, delete 연산은 최악의 경우 선형 시간이 걸린다고 이해할 수 있습니다.
어떤 원소를 찾는 연산은 얼마나 걸릴까요?
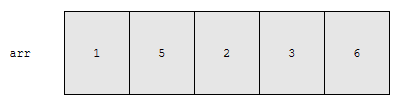
7을 찾아봅시다. 어떻게 찾아야 할까요? 1번째 원소부터 마지막 원소까지 7인지 아닌지 찾아야 합니다. 선형 탐색을 해야 하므로 비교 횟수는 n입니다. 그런데, 정렬이 되어 있다면 이야기가 달라집니다. 아래 배열은 오름차순으로 정렬되어 있습니다.
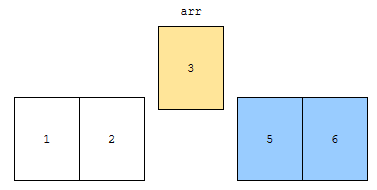
배열의 중간부터 시작합시다. mid 값인 3보다 7이 크기 때문에, 오른쪽에서 탐색합니다. 왜 오른쪽에서 탐색해도 될까요?
- 배열이 오름차순으로 정렬되어있습니다.
- 중간보다 왼쪽에 있다면, 중간보다 작거나 같은 값만 왼쪽에 있을 겁니다.
- 그런데 중간에 있는 값이 3이였네요?
- 그러면 중간보다 왼쪽에 있는 값은 3보다 작거나 같으니 탐색할 필요가 없습니다.
1 사이클이 돌 때 마다 탐색 범위가 절반으로 감소합니다. 배열 크기가 100만이라 해도 20 번 정도의 사이클만 돌아도 찾을 수 있을 정도입니다. 따라서, 길이가 n인 배열이 정렬되어 있을 때 비교 횟수는 log(n)이 됩니다.
여기까지 정리해 봅시다.
- insert, delete는 맨 뒤에 일어날 때 O(1), 중간 혹은 맨 앞에 일어나면 O(n) 입니다.
- 어떤 원소가 있는지 찾는 것은
- 정렬되어 있지 않으면 n번의 비교가 필요합니다.
- 정렬되어 있는 경우 log(n)번만에 비교를 할 수 있습니다.
- 배열은 k번째 원소를 (random access) 빠르게 찾을 수 있습니다.
- 기준 주소를 가지고 한번에 계산할 수 있기 때문입니다.