배열의 크기가 n일 때, O(n2)로 동작하는 몇 개의 정렬 알고리즘이 있습니다. 선택 정렬, 삽입 정렬, 버블 정렬이 대표적입니다. 이 글에서는 선택 정렬을 알아봅니다. 이 셋 중, 자주 보이는 알고리즘은 insertion sort인데요. 아래 글을 참고하시면 좋습니다.
- insertion sort에 대해서 알아봅시다. 링크
선택 정렬은 어떻게 동작하는가?
selection sort는 정수를 오름차순으로 정렬한다고 하였을 때, 아래와 같이 동작합니다.
- i번째 cycle일 때
- i번째 원소 a와 [i+1, n] 구간에 있는 원소 중 가장 작은 원소 b와 비교합니다.
- a가 b보다 크면, a와 b를 바꿉니다.
이것이 무슨 소리인가? 아래 그림을 봅시다.
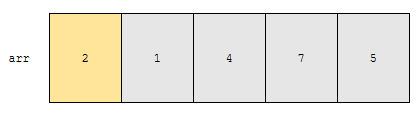
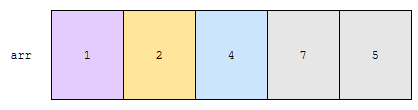
배열 arr에 2, 1, 4, 7, 5 순서대로 저장되어 있습니다. 저는 이 배열을 오름차순으로 정렬하려고 합니다. 배열의 크기 n은 5입니다. 1번째 cycle이 돌 때 아래와 같은 일이 일어납니다.
- 1번째 원소인 2
- [2, 5] 구간에 있는 원소 중 가장 작은 원소를 구합니다.
[2, 5] 구간에 있는 원소 중 가장 작은 원소는 1입니다. 제가 파란색으로 표시한 원소입니다.
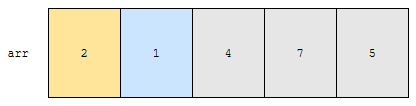
a가 2이고 b가 1입니다. a가 b보다 큰 상황인가요? 고로 두 원소를 바꿉니다.
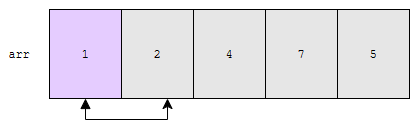
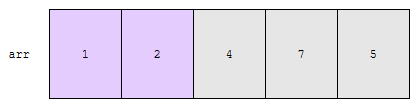
그러면, 1, 2, 4, 7, 5가 되고 사이클 1이 끝납니다. 이제, 보라색 구간은 정렬 완료되었습니다. 사이클 2로 가 볼까요?
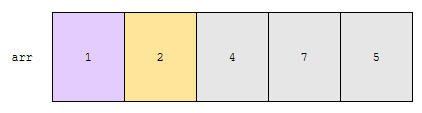
2번째 원소인 2와, 회색 구간에 있는 수 중 가장 작은 수를 뽑습니다. 회색 구간에 있는 것 중 가장 작은 것은 4입니다.
2 < 4인가요? 따라서 원소가 바뀌지 않습니다.
이렇게 사이클 2가 완료됩니다. 이런 식으로 사이클을 n-1번 돌면 정렬이 완료되는 것이 선택 정렬입니다. 시간 복잡도는 어떻게 될까요? i번째 사이클에 정렬되지 않은 n-i개의 원소 중 최소값을 고르는 연산을 하게 되므로, O(n2)가 됩니다.
정당성 증명해 보기
이 알고리즘이 정렬을 올바르게 할까요? 이걸 증명하기 위해서는 아래를 증명해야 합니다. n개의 정수로 이루어진 배열을 선택정렬로 오름차순 정렬할 때
- i번째 cycle에 i번째 요소에 업데이트 되는 요소는 아래 조건을 만족합니다.
- a1은 가장 작은 수이다.
- ai-1 < ai이거나 ai-1 = ai이다.
1번째는 자명합니다. 2번째가 문제입니다.
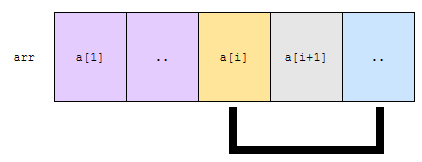
i번째 사이클이 돌 때 상황을 생각해 봅시다. 이 경우에는
- 노란색으로 표시한 원소
- 회색 부분 중, 제일 작은 원소
이 둘 중 가장 작은 것이 i번째 사이클이 끝났을 때 a[i]에 오게 됩니다. 즉, i번째 사이클이 끝난 이후 상황은 아래와 같이 됩니다.
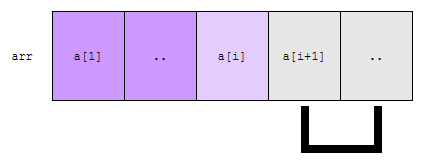
a[i]는 회색으로 표시된 구간에 있는 수들보다 작거나 같다. 그러면 이 회색 부분은 볼 필요가 없습니다. 이제 문제는 진하게 표시된 보라색 부분입니다.
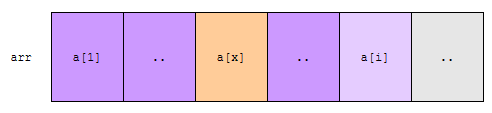
a[x]가 a[i]보다 크다고 하겠습니다. 이 상황을 #1이라 하겠습니다. 그렇다면 이 a[x]는 언제 뽑힌 걸까요? x번째 사이클에 뽑힌 것입니다. 이 상황으로 돌아가 보겠습니다.
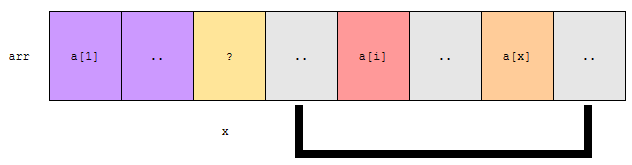
먼저, a[x]라는 값이 처음에 x번째 위치에 있지 않았을 때를 생각해 봅시다. 이 경우, 제가 표시한 회색 구간에서 주황색으로 표시한 게 뽑힐 수 있나요? a[x] > a[i] 이므로 그럴 수 없습니다. 최소한 a[x]는 뽑히지 않을 겁니다. 왜? a[x]보다 더 작은 a[i]가 있기 때문입니다.
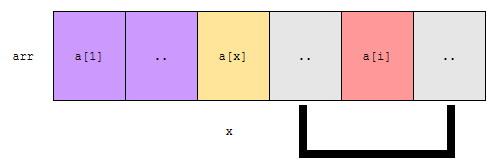
a[x]가 기존에 x번째 위치에 있었다고 해도 마찬가지입니다. 회색 구간에 a[i]가 있는데, 이미 a[i] < a[x]입니다. 따라서 x번째 사이클이 끝난 후에 a[x]는 x번째 자리에 있을 수 없습니다. 즉 #1과 같은 상황은 일어날 수 없고, 정렬이 정상적으로 수행됩니다.
stable sort인가?
그러면 선택 정렬은 stable 할까요? 아니라는 것을 손쉽게 알 수 있습니다.
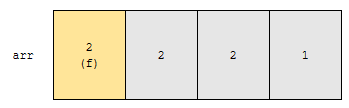
배열 arr에 2, 2, 2, 1 순서대로 있고, 오름차순으로 정렬해야 한다고 해 보겠습니다.
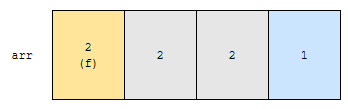
회색 구간에서 최소값은 1입니다. 그러면, 노란색으로 칠한 부분하고 1을 바꿀 겁니다.
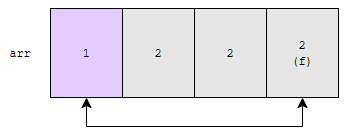
바꾼 후에는 위와 같이 됩니다. f라고 표시한 2가 맨 뒤로 갔습니다. 즉, 같은 우선순위를 가지는 원소에 대해, 정렬을 하기 전과 후의 순서가 다릅니다. 따라서 unstable 합니다.
코드
이제, 선택 정렬 코드를 간단히 보겠습니다.
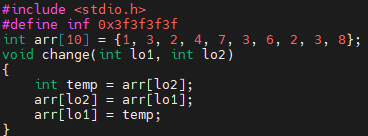
먼저, 크기가 10인 arr 배열이 있습니다. change 함수가 있는데요. lo1번째 원소와 lo2번째 원소를 바꾸기 위함입니다. c++을 쓰시는 경우, algorithm 헤더의 swap 함수를 이용하시면 됩니다.
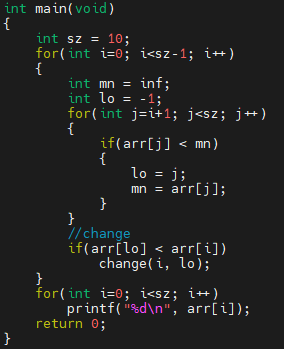
다음, for loop 부분이 핵심입니다. 사이클을 sz-1회 도는데요. 사이클을 돌 때 마다 어떻게 하나요? i+1번째 원소부터 끝의 원소 중 최소값을 가지는 원소를 찾아요. 이것을 mn이 들고 있어요. 다음에 arr[lo]가 arr[i]보다 작으면 이 둘을 바꿉니다.
실행 결과는 위와 같습니다.
안녕하세요.
문의드릴 게 있는데 메일 주소 하나 부탁드려도 될까요 ?
메일은 codingdog03@gmail.com 으로 보내주세요.
메일 드렸습니다. 확인 부탁드립니다.