유니온 파인드를 배우면서, 크루스칼 알고리즘을 배우게 됩니다. 그리디 알고리즘을 배우면 꼭 배우는 알고리즘입니다. 크루스칼 알고리즘 정당성 증명을 해 보겠습니다. 이 글에서는 명제 p가 참임을 증명하기 위해서, ~p가 거짓임을 보일 겁니다.
정당성 보이기
먼저 크루스칼 알고리즘은 아래와 같이 동작해요. 예를 들어, 모든 정점들을 연결하는 데 총 비용이 가장 낮게 연결하려고 해요.
- 가중치 오름차순으로 정렬해요.
- 가중치가 a에서 b를 연결할 때
- a와 b가 같은 집합에 속해 있으면 연결하지 않아요.
- 그렇지 않으면 연결합니다.
이 알고리즘이 정확하게 동작할까요? 이를 보여봅시다. 그리고, 제가 출제한 문제에서도 적용해 보도록 합시다.
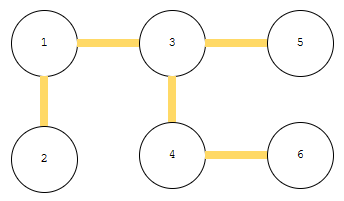
먼저, 크루스칼 알고리즘에 따라 선택한 트리는 위와 같습니다. 여기서 우리는 한 가지 가정을 할 거에요. 이 그래프가 최소 스패닝 트리가 아니다. 즉, ~p인 셈입니다. 이 그래프를 1번이라고 해 보겠습니다.

군청색 간선만 보겠습니다. 이렇게 선택해도 트리긴 하지요? 이 트리는 위 알고리즘에 따라 선택한 것이 아닙니다. 이것을 mst라고 하고, 2번이라고 할게요. 위 그림에서 X와 X’는 아래와 같은 특성을 가집니다.
- 간선 X는 1에는 속하지 않지만 2에는 속합니다.
- 간선 X’은 2에는 속하지 않지만 1에는 속합니다.
그래프 1이 최소 스패닝 트리가 아니고, 2가 최소 스패닝이 되려면 어떻게 되어야 할까요? 최소한 X는 X’보다 작아야 합니다. X와 X’이 같으면 둘 다 최소 스패닝 트리가 되기 때문에 안 됩니다.
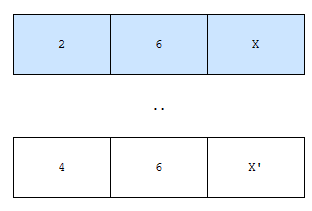
그런데 봅시다. X < X’이고, 가중치 오름차순으로 정렬했다면, 2에서 6을 연결하는 가중치가 X인 것이 4에서 6을 연결하는 가중치가 X’인 것보다 먼저 나옵니다. 그런데 1번 그래프는 어떻게 만들어 졌나요?
- 가중치가 작은 간선부터 나왔습니다.
- 가중치가 a와 b를 연결한다 했을 때
- a와 b가 같은 집합에 속해 있으면 뽑지 않습니다.
- 그렇지 않으면 뽑고 a와 b를 같은 집합에 넣습니다.
요런 알고리즘으로 만들어 집니다. 이 말은 1번 그래프를 만들 때 가중치가 X’인 것이 X인 것보다 먼저 나왔음을 의미해요. 그러면, 가중치가 X’인 것을 볼 때, 가중치가 X인 간선으로 연결되지도 않은 상황입니다. 사이클이 없으니, 가중치가 X’인 것으로 연결되겠네요.
그런데, 이렇게 했을 때, 그래프 1이 나오지 않습니다. 이 상황에서, 그래프 1이 언급하는 알고리즘으로 만들어 졌다고 합니다. 모순입니다. 그래프 1이 위 알고리즘으로 만들어 졌다면, 어떤 조건을 만족해야 하나요?
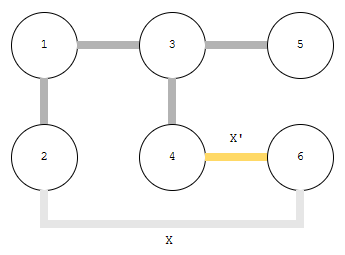
이 말인 즉슨, X’ < X를 만족하고 실제로 아래와 같이 나왔음을 의미합니다.
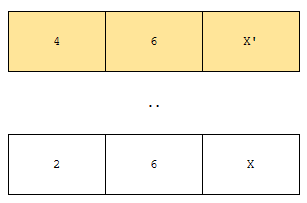
크루스칼 알고리즘 정당성 보여서, 올바르게 동작한다는 것을 보였습니다. 다른 관점에서 접근해 보겠습니다.
다른 관점에서 보기
간선 s를 선택하는 경우, s’를 선택하는 상황보다 손해를 안 본다. 제가 출제한 또 다른 문제의 키워드였습니다. 그렇다면, 위의 경우는 어떨까요?
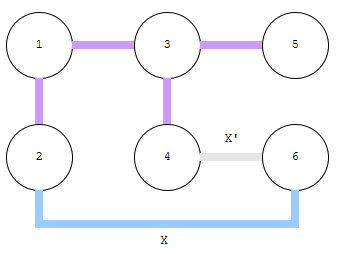
X’ 대신 X를 선택했다고 해 봅시다. 그렇다면 보라색 간선의 총합 + X가 됩니다. 그런데 X’을 선택할 때 보라색 간선들을 그대로 쓸 수 있어요.
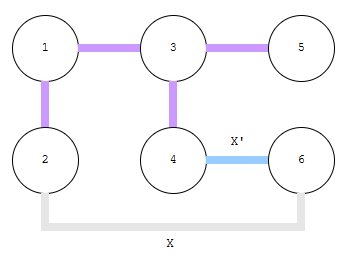
다른 점은 X 대신 X’ 이 더해진다는 것입니다. 두 상황의 공통점이 무엇인가요? X’보다 X가 크거나 같은 경우, X을 선택했을 때 최적의 해 보다 더 좋거나 같게 만들 수 있는 방법이 존재한다는 것입니다. 제가 출제한 문제는 이 관점에서 접근하면 보다 쉽게 풀이할 수 있습니다. 이제 제가 출제한 이 문제를 풀어보겠습니다.
가희와 여행가요 풀이
해당 문제는 2개의 factor가 있습니다.
- 연합했을 때 총 비용은 최소로 하고 싶다.
- 총 비용이 최소가 되게 하는 것이 여러 개가 있다면, 건설 시간을 최소로 하고 싶다.
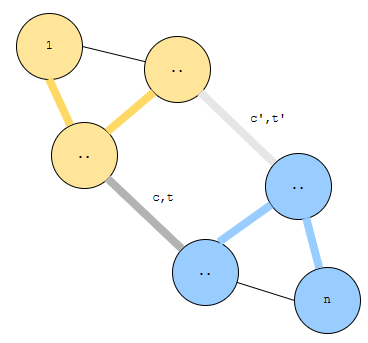
2개의 factor가 들어간단 말이죠? 조금 상황을 단순화 시키기 위해서, 노란색 집합과 군청색 집합을 연결하는 간선들을 생각해 보도록 합시다.
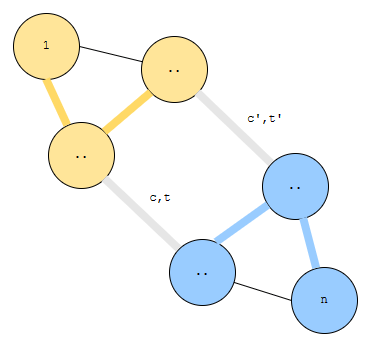
한 간선은 비용 c에 건설 시각 t입니다. 그리고 다른 간선은 비용 c’에 건설 시각 t’입니다. 두 가지 경우로 나눠 봅시다.
- c < c’인 경우
- 이 경우 무조건 비용 c에 건설 시각 t를 택하는 게 이득입니다.
비용이 c’이고 건설 시각이 t’인 것을 택했을 때, 노란색 + 군청색을 이은 게 최소라고 합시다.
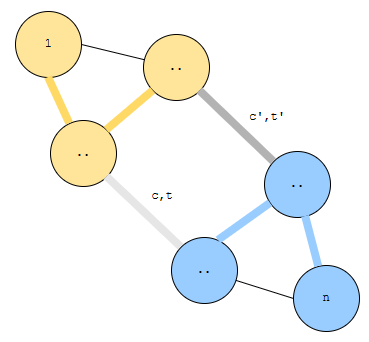
노란색의 비용 합을 y, 파란색의 비용 합을 b라고 합시다. 그러면 이 경우 y + b + c’이 나오게 됩니다. 그런데, 가중치가 c이고 건설 시각이 t인 간선을 선택하면 더 좋게 만들 수 있어요.
y + b + c가 나오는데 c가 c’보다 작기 때문에 비용이 더 작게 나옵니다. 비용이 c’이고 시각이 t’인 것을 선택했을 때 최선보다 더 좋게 택할 수 있어요. 남은 건 c = c’일 때입니다. 이 때에는 어떤가? 총 비용이 같기 때문에 시각에 따라 결정됩니다.
- 노란색 간선의 건설 시각 min을 yt
- 파란색 간선의 건설 시각 min을 bt
라고 합시다. 이 때, min(yt, bt, t)와 min(yt, bt, t’) 중 건설 시각을 작게 하라는 것이 문제인데요. 건설 시각이 다르다면, (즉 t와 t’이 다르다면) 당연하게도, 건설 시각이 작거나 같은 쪽을 택하는 게 이득임을 알 수 있어요. 즉, 아래와 같이 정렬하고 크루스칼을 수행하면 됩니다.
- cost가 작은 간선이 먼저 나오게
- cost가 같다면 건설 시각이 작은 간선이 먼저 나오게