제가 최근에 연 모의 코딩테스트에서, mst 문제를 출제하였습니다. mst 하면 유니온 파인드로 많이 구축하시는데요. 대회 몇 일 안 남겨두고 통과되지 말아야 할 코드가 통과되는 현상을 발견했습니다. 검수진 분들이 핵 당해야 할 코드를 많이 넣어주신 덕분이였습니다. 코드를 분석하고 저격 데이터들을 추가했는데요.
이 글에서는, union find by rank 기법을 보면서, 잘못된 코드는 어떤 식으로 저격이 가능한지 알아보겠습니다.
union find by rank
보통, path compress로, 유니온 파인드를 구축하는 경우가 많습니다. 빠르기 때문입니다. 하지만, 이 방법만 있는 것은 아니고, rank 기반의 방법도 있어요. 이 방법을 간단하게 알아볼 거에요. 예제에 쓰이는 각 변수들은 아래와 같습니다.
- h
- rank를 의미합니다. 이 예제에서는 높이 기반을 사용합니다.
- par
- par[x]의 경우, x의 부모를 저장합니다. 루트라면 0입니다.
그리고 함수 중에 _merge가 있는데요. 이 함수는 x와 y를 받습니다. 이 둘은 _find로 찾은 포레스트의 root를 넣습니다.

그림 1은 코드입니다. 8번째 줄이 중요한데요.
- h[x] 보다 h[y]가 같거나 크다면
이라는 조건이 걸려 있어요. 그렇다면 x의 부모를 y로 설정하라고 되어 있습니다. 그게 아니라면, y의 부모를 x로 설정합니다. 이를 도식화 해서 설명해 보겠습니다.
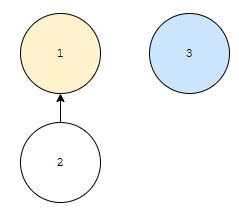
위와 같이 구성된 포레스트 2개가 있다고 해 보겠습니다. 현재 par[2]가 1인 상황입니다. 1의 rank는 1이고, 3의 rank는 0입니다. 높이 기반으로 보기 때문에 그렇습니다. 1과 3을 merge 할 때 어떻게 할까요? h[3]보다 h[1]이 같거나 크기 때문에, par[3]이 1이 됩니다.
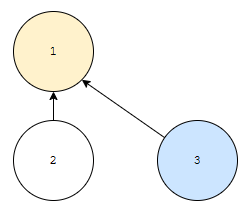
그러면, 위 그림과 같이 연결 관계가 구축됩니다. height가 작은 쪽이 큰 쪽에 합쳐졌습니다. 이 경우, 어느 root의 rank가 변하지 않습니다. 다시, 이제 두 친구가 동일한 rank를 가지는 경우를 생각해 봅시다.
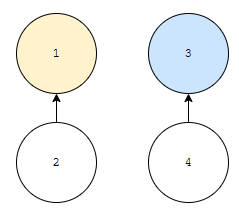
이 경우는 어떻게 합치면 될까요? h[3]보다 h[1]이 같거나 큽니다. 이 경우에는 같은 상황이니까요.
- par[3]의 값을 1로 설정합니다.
- 루트가 1인 포레스트의 높이가 증가했으니 h[1]을 하나 증가시킵니다.
이 단계를 수행하면 됩니다.
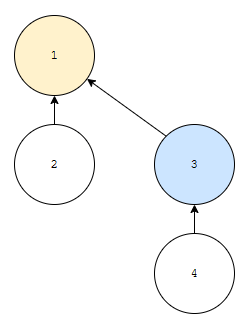
그러면 위 그림과 같이 됩니다. _find(4)를 호출하면 4, 3, 1을 거치게 됩니다. 고로, 이 때가 최악일 겁니다. 이렇게 union find를 했을 때 최악 복잡도가 어떻게 될까요? _merge는 별 게 없으므로, _find의 복잡도를 보아야 하는데, 포레스트의 높이와 관련이 있습니다.
시간 복잡도 계산해 보기
포레스트 2개가 합쳐져서 큰 포레스트가 만들어졌다고 합시다. 높이는 언제 증가할까요?
- 높이가 다른 두 포레스트가 합쳐졌을 때
- 높이가 같은 두 포레스트가 합쳐졌을 때
후자의 경우에 증가하겠지요? 포레스트 1의 높이가 h1이고, 포레스트 2의 높이가 h2였어요. h1 > h2인 상황에서는 포레스트 2의 root의 부모가 포레스트 1의 root가 됩니다. h2 + 1이 h1보다 같거나 작습니다. 따라서, 합쳐진 포레스트의 높이는 h1입니다.
그런데, h1과 h2가 같은 경우에는 어떤가요?
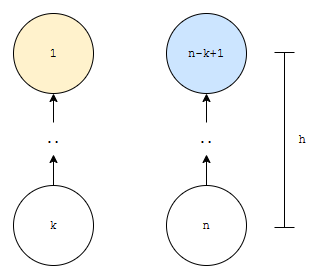
위 그림과 같은 경우입니다. n-k+1의 부모를 1로 설정해 보겠습니다.
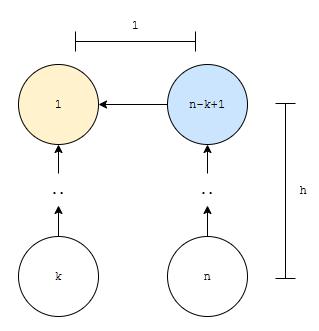
그러면 합쳐진 포레스트의 높이는 h+1이 됩니다. 이 그림에서는 _find(n)을 호출할 때 탐색을 n을 포함해서 총 h+1개의 노드를 탐색할 겁니다. 이 말인 즉슨 합쳐지기 전에는 _find(n)을 호출했을 때 n을 포함해서 총 h개의 노드를 탐색했는데, 합쳐진 후에 하나만큼 증가한 것이 됩니다.
즉, 두 포레스트의 높이가 같을 때 합쳐진 이후에 _find(x)의 탐색 노드 개수가 많아야 하나 증가합니다. 이러면 어떻게 될까? 제일 빠르게 증가하는 케이스를 보면 됩니다.
높이가 0인 두 포레스트가 있습니다. 합쳐진다면 높이가 1이 되겠네요.
다음에, 또 요렇게 포레스트가 있어요. 1자 포레스트. 이 둘이 합쳐지면, 높이가 2가 됩니다.
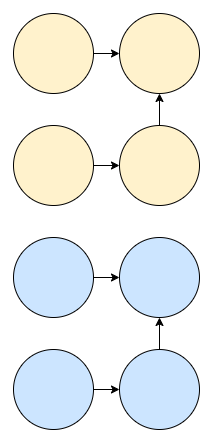
다음에 이 두 포레스트가 합쳐지면, 높이가 3이 되겠네요. 제일 최악의 경우에 해당 방식으로 merge를 하면, 크기가 2k라면 구축된 포레스트의 높이가 k-1가 됩니다. 높이가 로그 스케일이 됩니다. 고로, 상당히 빠르게 동작하게 됩니다.
즉, rank가 작은 쪽을 큰 쪽에 합치면 효율적으로 동작합니다. small to large trick이 잘 알려져 있으니, 찾아보시는 것도 도움이 되겠습니다.
잘못된 union find by rank 코드
그러면 이 코드는 어떨까요? 시간 내에 제대로 동작할까요?

아쉽게도 그렇지 않습니다. 왜 그럴까요? h[x]보다 h[y]가 크거나 같을 때, y의 parent를 x로 설정하고, 그렇지 않으면 x의 parent를 y로 설정했어요. 반대로 설정한 건데요. 이러면 어떻게 되는가? 아래와 같이 합쳐질 때 문제가 발생해요.
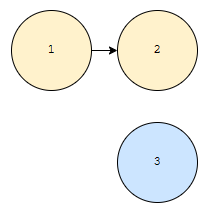
h[3]보다 h[2]가 크거나 같으므로, 2의 부모가 3이 됩니다.
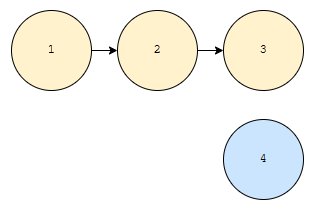
이 상태에서 다시, 4와 합쳐 봅시다. h[4]보다 h[3]이 같거나 크므로, 3의 부모가 4가 됩니다. 이 상황이 계속 반복되면 1자형 트리가 만들어 지겠네요. 고로, 손쉽게 시간초과가 날 수 있습니다. 이것 말고도 경로 압축 없이, rank 고려하지 않고 무작정 합치는 경우도 비슷하게 1자 포레스트가 생성되게 하게 만들어서 저격할 수 있습니다.