백준에서 n과 m 시리즈는 백트래킹을 연습하기 좋은 문제입니다. 이들을 응용한 문제가 코딩 테스트에 출제되는데요. n과 m 1 문제를 풀기 쉽게 해 주는 python itertools permutations 함수에 대해 알아보겠습니다.
permutations 함수 설명

먼저, permutations를 보겠습니다. 이 함수는 2개의 인자를 받아요.
- iterable
- 뽑을 후보들이 저장되어 있는 집합
- r
- 집합에서 몇 개를 뽑을 것인지.
서로 다른 n개의 원소에서 r개를 중복 없이, 순서 중요하게 생각하는 것을 Permutation 이라 합니다. 순서 정보가 중요하지 않는 것이 Combination 입니다. 순서가 중요하다는 말이 무슨 말일까요? 1, 2, 3, 4, 5로부터 2개의 수를 뽑는다고 해 볼게요.
그러면 1, 3 순서대로 뽑을 수도 있을 겁니다. 하지만, 반대의 순서로 뽑을 수도 있습니다.
순서가 반대가 되었나요? permutation은 이 둘을 다르게 취급합니다. 왜? 1과 3을 뽑았다는 정보 뿐만이 아니라, 어느 순서대로 뽑았는지도 중요하게 여기기 때문입니다. 이 “순서”에 대한 개념은 제가 출제한 문제에도 중요하게 다루어 졌으므로 개념을 잡고 가시는 게 좋아요.
이 함수는 yield가 있는 것으로 보아서
- 현재 permutation을 돌려주고
- 다시 호출이 되면 다음 permutation을 돌려주고
이렇게 작동을 하는 것임을 알 수 있겠네요. tuple을 돌려주니, 실제 원소들에 접근하기 위해서는 for ~ in 구문으로 접근해야 합니다.
예제 같이 보기
예제 프로그램을 보도록 합시다.
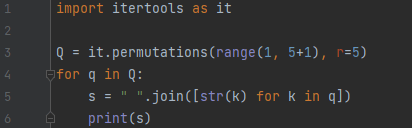
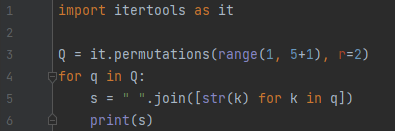
python itertools permutations 함수에 인자 2개를 넣었습니다.
- range(1, 5+1)
- r = 5
무엇을 의미하는 것인가? 집합이 되는 것은 range 객체로 1, 2, 3, 4, 5를 의미합니다. 이 중, 5개의 원소를 뽑습니다. 다음에 순서를 고려하겠다는 의미입니다. 가짓수는 5P5 = 5! = 120가지가 나옵니다.
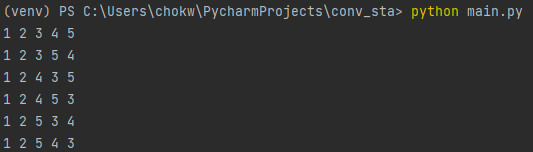
1 2 3 4 5가 나온 후에 또 다시 호출되었기 때문에 1 2 3 5 4가 호출됩니다. 이 둘이 다른 건가요?
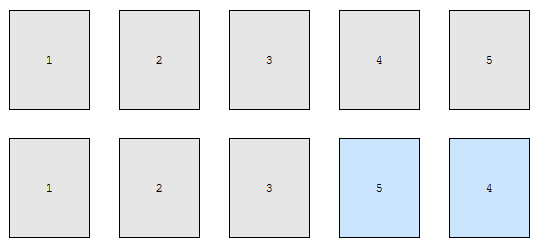
4와 5의 순서가 다릅니다. 따라서, 다르게 취급합니다.
이제, 2번 프로그램을 보겠습니다. 집합은 1부터 5까지 나오고요. 이 중 2개의 원소를 뽑아요. 역시 퍼뮤테이션이므로 순서 중요하겠네요. 이건 결과가 어떻게 나올까요? 총 몇 가지 결과가 나올까요? 5P2이니까, 가짓수는 20가지가 나올 거에요.
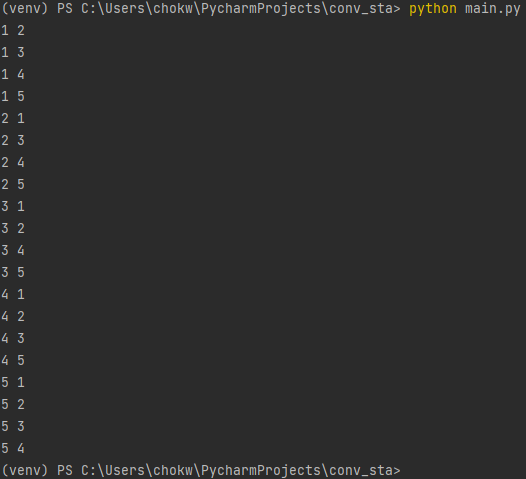
1 2와 2 1이 나왔음을 볼 수 있어요. 똑같은 이유입니다. 두 순열은
- 1과 2가 뽑힌 것은 같습니다.
- 그런데, 순서가 다릅니다.
그렇기 때문에, 1 2와 2 1이 나오게 된 것입니다. 이걸 brute force, back tracking의 어느 문제에 써먹는가? 사실 단독으로 쓰이는 경우는 잘 없어요. “순서”가 중요하다는 것을 읽어낼 수 있는 능력을 요하는 문제가 자주 보일 뿐이지. 제가 출제했던 문제에 해당 개념을 써먹을 수 있습니다.
예제 문제
제가 출제한 문제를 간단히 봅시다. 보면 각 사람마다 카드를 내는 순서는 정해져 있습니다. 그렇다면 카드 a가 1번 사람이 내고, 카드 b를 2번 사람이 내야 한다면, 카드 a 다음에 b를 내는 경우, b 다음에 a를 내는 경우 이 2개가 가능합니다.
여기서 궁금한 것은, 이 경우에 카드를 내는 순서가 중요하냐는 것입니다. 카드 a와 b가 아래와 같은 연산이 있었다고 해 보겠습니다.
- add d
- del 1
원본 문자열이 “a”였다고 해 보겠습니다. a 다음에 b를 수행하면 어떻게 되나요?
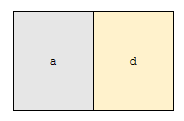
먼저 add d에 의해, 문자열 “a”가 “ad”가 됩니다. 다음에 1번째 원소를 제거합니다. 따라서, 아래와 같이 됩니다.

따라서, 최종적으로 “a”가 됩니다. 하지만, b 다음에 a를 수행하지 못합니다. “a”는 길이가 1이기 때문에 del 0을 수행하지 못해요. 즉, 카드 a에 있는 연산과 카드 b에 있는 연산의 교환 법칙이 성립하지 않아요. 심지어, add 연산 간에도 교환 법칙이 성립하지 않아요.
연산 a가 ADD g였고, 연산 b가 ADD h였다고 해 볼게요. 원본 문자열이 “c”였고요. a 다음에 b를 수행한 경우에는 아래와 같이 됩니다.
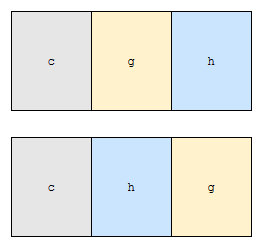
당연하게도 결과가 다르게 나와요. 따라서, 순서가 중요하다고 할 수 있어요. 이 개념은 상당히 중요하고, 저 또한 백준 모의 코딩테스트에 많이 출제했으니 반드시 알아두세요.