저번 시간에 count sort를 한 적이 있었습니다. 어떤 것이였나요? 수의 최대값과 최소값의 차이가 작을 때 count 배열을 두어, 처리할 수 있었던 것이지요. 만약에 이 차이가 20억이면 어떨까요? 당연하게도, 어떤 수가 몇 개나 있는지 저장할 수 없을 것입니다.
radix sort (기수 정렬)을 사용하면 이 점을 해결할 수 있습니다. 이 글에서는 이에 대해 알아보도록 하겠습니다.
- counting sort
- radix sort [현재글]
하위 자리부터 정렬하기
20억이라는 큰 수는, 65536의 제곱보다는 작습니다. 65536은, 우리가 count 배열에 담아두기에 적합한 size입니다. 만약, -10억에서 10억까지의 범위를 가지는 수들로 이루어진 배열을 정렬해야 한다면, 어떻게 하면 될까요?
배열에 있는 모든 수에 10억을 더하고 시작합니다. 그러면, 65536a + b 꼴로 표현이 가능합니다. 단, a와 b는 0 이상 65536 미만의 정수입니다. 여기서 시작합니다. 이렇게 표현될 때, a는 65536으로 나누었을 때의 몫, b는 나머지라고 생각할 수 있습니다.
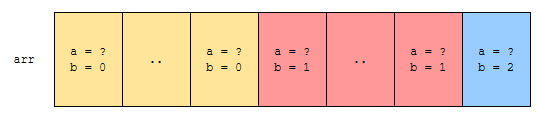
먼저, 나머지가 0인 것, 1인 것, 2인 것 순서대로 정렬합니다. 즉, 나머지가 작은 순으로 먼저 정렬합니다. 그 다음에는 어떻게 하면 될까요? 첫 번째 원소부터 차례대로 훑으면서, 몫이 작은 순으로 정렬하면 됩니다.
- 나머지 오름차순으로 정렬합니다.
- 몫 오름차순으로 정렬합니다.
만약 나머지 값인 b에 대해서 정렬이 되었다고 해 보겠습니다.
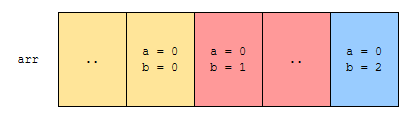
그러면 a가 같을 때, b가 더 큰 것이 먼저 나올까요? 그러지 않습니다. 왜? b가 더 큰 것은 뒤에 나오는 것이 자명하기 때문입니다. 이미 b에 대해 오름차순으로 정렬했기 때문입니다. 한 개의 예제를 가지고 시뮬레이션을 해 보도록 하겠습니다.
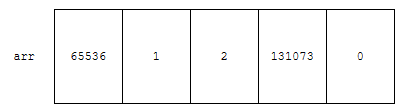
배열이 요렇게 있었습니다. 먼저, 나머지 오름차순으로 정렬해 봅시다.
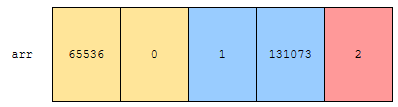
그러면, 65536, 0이 먼저 나오고, 다음에 1, 131073, 그 다음에 2가 나옵니다. 2순위 기준으로 먼저 sort 했다는 것이 중요합니다. 다음에, 이 상태에서 몫을 기준으로 정렬하겠습니다.
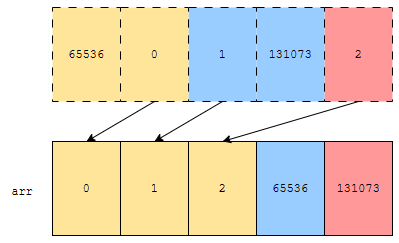
그러면, 0, 1, 2가 먼저 나오고, 다음 몫이 1인 65536, 그 다음에 몫이 2인 131073 이렇게 정렬이 됩니다. 중요한 것은 그림에 있는 화살표가 교차되지 않았다는 것입니다. 만약에, 화살표가 교차되었다면, stable 하지 않습니다. rank가 같은 데 자리가 바뀌었기 때문입니다.
즉, 나머지를 기준으로 먼저 stable sort를 하고, 몫을 기준으로 stable sort를 하면 문제 없이 돌아갈 것이 자명합니다. 여기까지 코드를 보겠습니다.
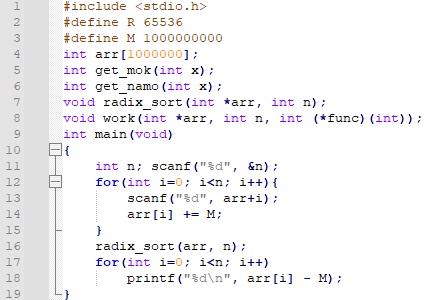
먼저, -10억 ~ 10억 사이의 수가 들어온다고 하였을 때 처리하는 부분입니다. 14번째 줄과, 18번째 줄은 왜 있는 것인지는 아실 것이라 생각합니다. 8번째 줄의 3번째 인자는 함수 포인터인데요. 몫을 리턴하는 경우와, 나머지를 리턴하는 경우가 있기 때문에, function pointer로 rank를 불러오는 부분을 처리하였습니다.
이제, radix sort 함수와 get_mok, get_namo 함수 내부로 들어가 봅시다.

먼저 get_mok은, 65536으로 나누었을 때 몫을 구합니다. get_namo는 나머지를 구해요. bit 연산으로 보다 빠르게 처리했음을 알 수 있습니다. 다음, radix_sort 함수의 내부를 보면, work를 2번 호출합니다. 그런데, 3번째 인자가 달라요. 한 번은 get_namo를, 다른 한 번은 get_mok을 호출하는데요. 이는, rank를 구할 때 먼저 나머지를 기준으로 정렬하고, 그 다음에 몫을 기준으로 정렬하기 때문입니다.
rank 별로 원소 모으기
work 함수는 rank 별로 원소를 모으는 역할을 합니다. 사실, 이게 제일 중요합니다. 이것을 어떻게 해야 할까요?
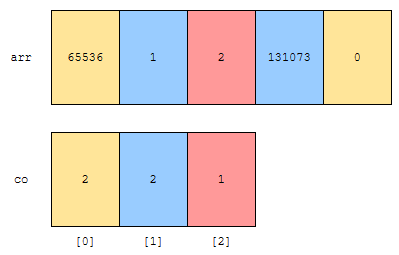
먼저 rank가 x인 것의 개수를 셉니다. 예를 들어 rank(x)가 x의 나머지라고 해 보겠습니다. 그러면,
- 나머지가 0인 것과 1인 것의 개수는 2입니다.
- 나머지가 2인 것의 개수는 1입니다.
따라서 co 배열은 위 그림과 같이 나오게 됩니다.
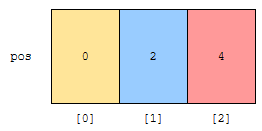
이를 토대로, rank가 x인 수가 최초로 나오는 지점을 pos[x]로 정의합니다. 이 경우, rank(x)를 x로 나누었을 때 나머지로 정의하였습니다. rank가 0인 것이 먼저 나오고, 1인 것이 다음에, 2인 것이 그 다음에 나온다면
- rank[0]의 최초 pos 값은 0입니다.
- rank[1]의 최초 pos 값은 rank가 0인 것의 개수입니다.
- rank[2]의 최초 pos 값은 rank가 0, 1인 것의 개수입니다.
이는 누적합 배열로 처리 가능합니다. 이렇게 구축해 놓은 것이 어떻게 쓰일까요?
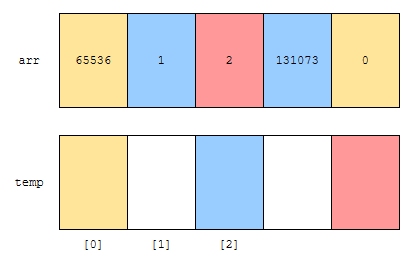
노란색은 rank가 0인 것, 파란색은 1인 것, 빨간 색은 2인 것입니다. 먼저, 65536을 읽습니다. rank가 0이지요? 따라서, 진한 노란색이 가리키고 있는 0번째 위치에 넣습니다.
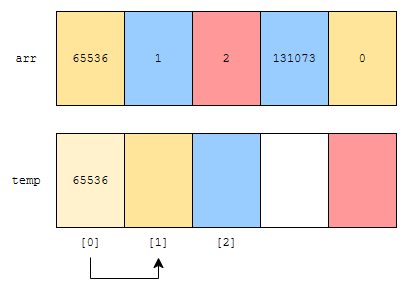
temp에, 65536이 들어간 상태입니다. 그 다음에 어떻게 되었나요? 노란색이 가리키는 것이 하나 증가했습니다. 이제 1을 읽어볼까요?
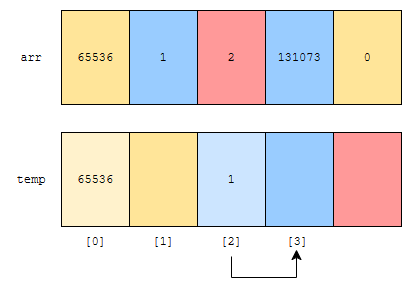
1을 65536으로 나누었을 때 나머지는 1이므로, 1의 rank는 1입니다. 따라서, 2번째 위치에 1이 들어가고, 군청색은 그 다음 원소를 가리키게 됩니다. 이런 알고리즘으로 모든 원소에 대해서 다 채워나가면, 아래와 같이 채워집니다.
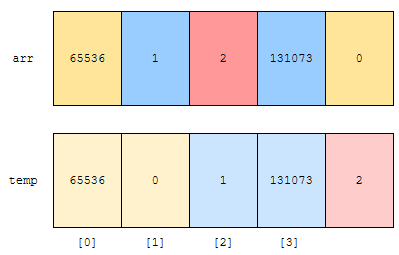
이 과정 얼마나 걸릴까요? 배열의 크기가 n이고, radix 진법으로 처리한다면 O(n + radix)만큼 걸립니다. 이제 코드를 볼게요.

work 함수는 크게 4부분으로 이루어져 있습니다. 여기서, func는 rank를 구하는 함수입니다.
- rank가 x인 것을 count 한다.
- 누적 배열 pos를 구축한다. 이를 토대로 rank가 x인 수가 들어갈 위치를 알 수 있다.
- 우리는 pos를 알기 때문에
- rank가 t인 수의 위치가 pos라면 pos 번째에 집어넣는다.
- 그리고 pos[t]의 값을 증가시킨다.
- 원본 배열에 처리 결과를 복사한다.
이 글에서 1 ~ 3번까지 개략적인 알고리즘을 설명하였습니다. radix sort는 work를 호출하는 횟수에 지배됩니다. work의 시간 복잡도는 O(n + radix)이고, work의 호출 횟수는 최대값과 최소값의 차이에 로그 radix를 씌운 것입니다. radix가 크고, 최대값과 최소값의 차이가 20억이나 900경이면, 그리 크지 않으니, O(n + radix)라고 보셔도 됩니다.