정렬해야 할 수의 범위가 작을 때, 특정한 수가 몇 번 나왔는지 count 하는 것만으로도 정렬할 수 있지 않을까요? 이 글에서는 계수 정렬에 대해 알아봅니다. 그리고, 이 아이디어를 확장하, radix sort를 사용할 수도 있는데요. 다음 글에서 알아봅니다.
- counting sort [현재글]
- radix sort
빈도수를 count 하기
먼저, counting sort는 최소값과 최대값의 차이가 작을 때 사용할 수 있습니다. 크면 사용할 수 없어요. 예를 들어, 최소값이 10^8이고, 최대값이 10^8+20이라고 합시다. 최소와 최대의 차이가 20입니다. 고로, 20개의 수가 몇 개 나왔는지 배열에 저장하기만 하면 됩니다.
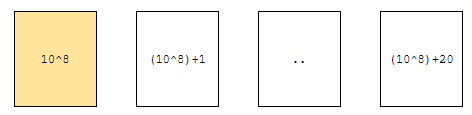
그런데 문제가 하나 있습니다. 1000만부터, 1000만 + 20이 나오는 배열을 정렬하기 위해서, 크기가 1000만이 넘어가는 count 배열을 만들 필요가 있을까요? 그렇지 않습니다.
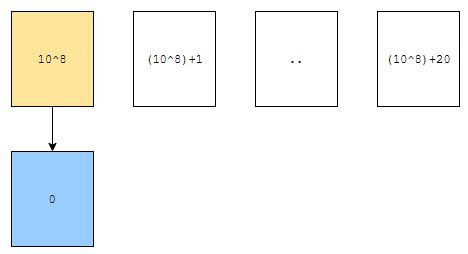
단지, 우리는 최소값 1000만에 대해, 0으로 mapping을 하면 됩니다. 그러면, 1000만 20은 어떤 값으로 mapping 하면 될까요?
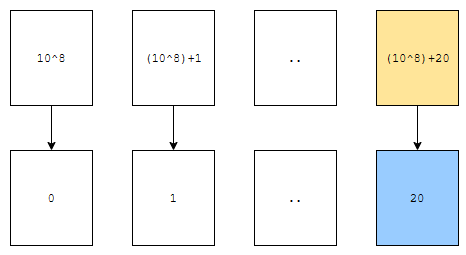
20으로 mapping 하면 되겠지요? 즉, 1000만 20이 나온 횟수는 count[20]에 저장하고 있으면 됩니다. 여기까지 정리해 봅시다.
- 배열에 등장하는 수의 최소값을 min 이라고 합시다.
- x가 등장하는 횟수는 count[x – min]에 저장하면 됩니다.
즉, 최소값 min이 나온 횟수를 count[0]에 저장하면 됩니다. 배열 -2, 2, -3, 1, -1을 count 배열에 저장해 봅시다. 최소값이 -3인가요? 따라서, 아래와 같이 mapping이 됩니다.
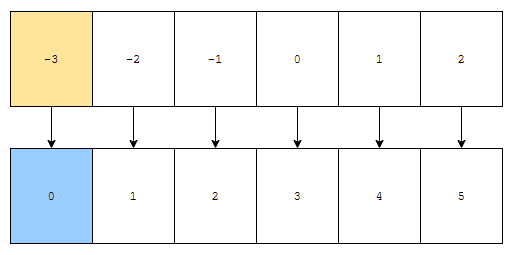
-3이 나타나는 빈도수는 count[0]에 저장됩니다. -2가 나타나는 빈도수는 count[1]에 저장되겠네요. 이제, 원본 배열을 훑으면서, count 배열에 수가 몇 번 나타났는지 저장합니다.
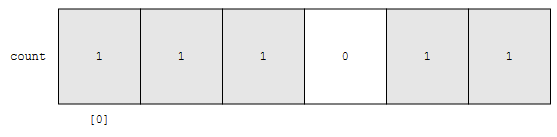
이제 빈도 배열을 다 채웠습니다. 이제, 다 채워진 배열을 순회할 일만 남았습니다.
count 배열 순회하기
어떤 수 x가 k개 있다는 정보를 count[x-min]에 채웠습니다. 이제 이걸 빼 봅시다.
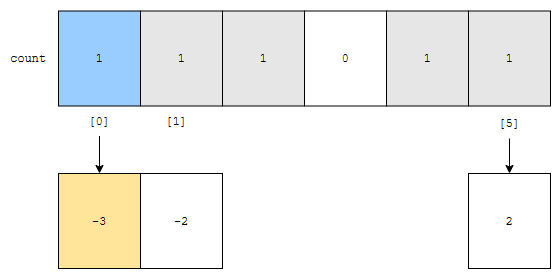
min 값이 -3이였어요. 그렇기 때문에, count[x]에는, x+min의 빈도가 저장되어 있습니다. count[0]에 1이 저장되어 있다는 의미는, 0-3의 값인 -3이 1번 나왔다는 의미입니다. 따라서, -3이 1번째로 빠지게 됩니다.
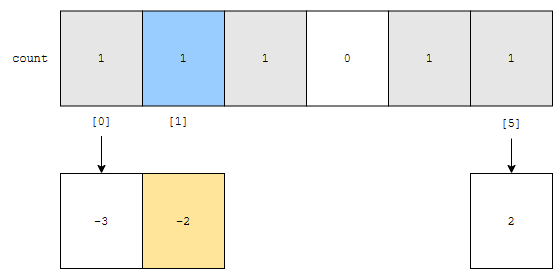
다음 count[1]에도 1이 저장되어 있었습니다. min 값이 -3이였기 때문에, 이 말은 -2가 원본 배열에 하나 있었다는 의미입니다. -2가 2번째로 빠지겠네요. 이런 식으로 계속 수를 빼다 보면 어떻게 될까요? 마지막에, 2가 하나 빠지겠지요?
따라서, -3, -2, -1, 1, 2 순으로 정렬되게 됩니다.
counting sort 코드 보기
그러면 코드로 간단하게 보도록 하겠습니다. 정렬해야 할 배열에 -10만부터, 10만까지 나온다고 해 보겠습니다. 그러면, 최소가 -10만이기 때문에, mn의 값은 -10만으로 설정됩니다.
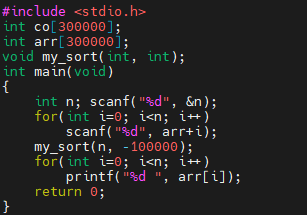
이제, 초기화 하는 부분을 볼게요. co 배열의 크기를 잘 보셔야 하는데요. 최소값인 -10만보다 크거나 같고, 최대값인 10만보다 작거나 같은 정수의 개수는 20만 1개입니다. 이보다 크거나 같은 30만개의 원소를 가지는 배열을 선언했음을 볼 수 있어요.
즉, counting sort의 공간 복잡도는 배열의 최소값을 min, 최대값을 max라 했을 때, O(max-min+1)이라는 의미입니다.
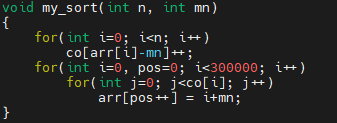
이제 정렬하는 부분을 볼게요. mn은 원본 배열에 나오는 최소값 이에요. 1번째 for loop에서 count 배열에 무언가를 채우고 있어요.
- 배열의 값이 x일 때
- co[x – mn]을 하나 증가시키고 있어요.
이는, co[x]를 x + mn이 나오는 횟수로 정의해서 그래요. 예를 들어, mn이 -10이라면, co[0]을, 0 + (-10)이 나온 횟수로 정의하고 있기 때문이에요. 최소값이 나온 회수를 co[0]에, 최소값 + 1이 나온 횟수를 co[1]에 저장해서 그런 것입니다.
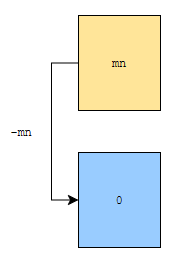
노란색은 실제 수이고, 군청색은 해당 수가 나타난 빈도를 저장한 배열의 위치라고 생각하시면 되어요. 이제, 출력을 할 거에요. 역순으로 변환하면 되겠지요?
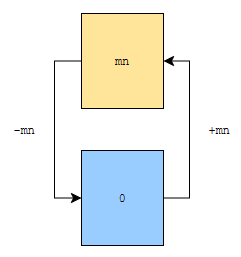
co[x]에 k가 저장되어 있었다면, 실제로 x+mn이 k번 나온 것이 됩니다. 이 변환은 2번째 for loop에서 하고 있어요.
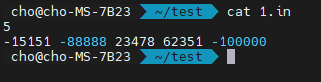
이제 간단하게 입력을 집어넣어 봅시다. -15151, -88888, 23478, 62351, -100000 이렇게 5개의 수가 저장된 배열이 있어요. 정렬해 볼까요?

정렬이 제대로 되었음을 확인할 수 있어요. 그러면, counting sort 알고리즘의 복잡도는 어떻게 될까요? 당연하게도, 최소값부터 최대값까지 몇 개나 저장되었는지 확인해야 합니다. 이를 배열을 모두 돌면서 해야 하지요. 그리고, count 배열을 scan 할 때도, 최소값부터 최대값까지 모두 scan 해야 합니다. 그렇기 때문에, 배열의 크기가 n이고, 최소값이 min이고 최대값이 max일 때, 계수 정렬의 공간 복잡도와 시간 복잡도는 아래와 같이 나오게 됩니다.
- 공간 복잡도는 O(max – min)이 됩니다.
- 시간 복잡도는 O(n + (max – min))이 됩니다.
중요한 것은, max와 min의 차이가 너무 클 때에는 쓸 수 없다는 것입니다.