백준에서 k번째 작은 수 찾기 알고리즘 문제를 볼 수 있어요. 예를 들어 이런 문제가 있습니다. 수가 n개 있다면, k번째로 큰, 혹은 작은 수를 찾는 문제인데요.
- radix와 bucket을 응용해서 O(n)에 푸는 방법
- median of median
등으로 해결을 할 수 있음이 알려져 있긴 해요. 이 중, median of median은 다음에 알아보는 것으로 하고요. 보다 쉬운 1번째 방식을 이 글에서 소개하고자 해요.
몫 count 누적 시키기
흔히, 누적합이라고 불리우는 방식입니다. 위에 링크를 걸어드린 문제는 수가 -10억부터, 10억까지 나올 수 있어요. 이는 65536의 제곱보다는 작은 숫자입니다. 우리는 k번째로 큰 수를 찾는 것이지, 정렬을 하는 것이 아닙니다. 즉, selection1을 하는 것이기 때문에, 아래와 같은 아이디어를 생각할 수 있습니다.
- 원본 수에 10억을 더하자.
- 그러면 65536a + b의 꼴로 나타낼 수 있다. (단, a와 b는 0이상 65536 미만의 정수)
- a값을 count 해 놓으면, k번째 수의 후보해는 줄일 수 있다.
- 이 후보해들을 가지고 b값을 집계하면 된다.
간단한 아이디어입니다. 왜 65536을 선택했는가? 적당히 큰 수이기도 하면서, 나머지와 몫 연산을 할 때, 비트 연산을 사용할 수 있기 때문입니다. 아이디어를 도식화 해 보겠습니다.
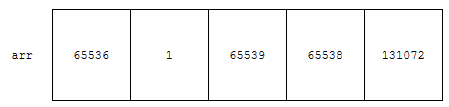
먼저, 배열 arr에는 수 5개가 있습니다. 65536, 1, 65539, 65538, 131072 이렇게 5개입니다. 저는 이 수들 중 3번째로 작은 수를 구하려고 합니다. 이 수들은 65536a + b 꼴로 나타낼 수 있습니다. 즉, 65536으로 나누었을 때 몫이 0인 것의 개수, 1인 것의 개수 등을 1번 순회하면 구할 수 있습니다.
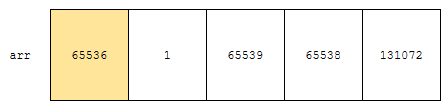
먼저 65536을 볼까요? 65536을 65536으로 나눈 몫은 1입니다. 고로 몫이 1인 수의 개수가 하나 증가합니다.
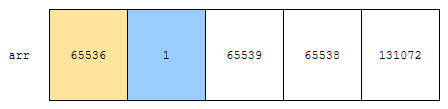
다음, 1을 보겠습니다. 이것을 65536으로 나누면 몫은 0이지요? 따라서 몫이 0인 수의 개수가 하나 증가합니다.

계속 순회해 봅시다. 65539와 65538이 나오네요. 이들의 몫은 1이에요. 따라서, 몫이 1인 수의 개수는 2가 증가하게 됩니다.

다음에 131072를 볼 거에요. 이 수를 65536으로 나누면 몫이 2에요. 따라서, 몫이 2인 수의 개수는 1이 증가해요. 여기까지 카운트 한 결과를 볼게요.

65536으로 나누었을 때 몫이 0, 1, 2인 수를 count 한 거에요. 3번째로 작은 수를 찾으라고 했습니다.
- 몫이 0인 것은 후보해가 될 수 없어요. 누적 1개이기 때문이에요.
- 몫이 1인 것은 후보해가 되나요?
- 이미 몫이 1인 것보다 작은 것이 1개 있었고
- 몫이 1인 것이 3개 있었습니다.
- 몫이 1인 것 중 제일 큰 것이 4번째로 작은 수가 됩니다. 3은 4보단 작습니다.
따라서, 몫이 1인 수 중 하나가, 3번째로 작은 수가 됩니다. 우리는 위 과정을 통해서 65536으로 나누었을 때, 몫이 1인 수로 후보해를 줄였습니다. 그 다음에는 어떻게 해야 할까요?
나머지 count 하고 누적시키기
우리는 65536으로 나누었을 때, 몫이 1인 수들로 후보해를 줄였습니다.
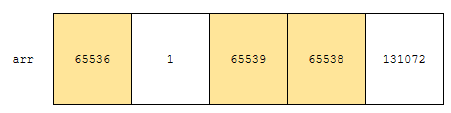
즉, 그림에서 탐색해야 할 부분은 노란색 부분인 셈입니다. 노란색 부분은 2번째로 작은 수부터 나오기 때문에, 이 부분은 처리해 주셔야 합니다. 이제, 노란색으로 표시한 것만 탐색해 봅시다. 흰색 수들은 몫이 1이 아니므로 이 단계에서 고려할 필요가 없습니다. 이들은 몫이 모두 같으니, 65536으로 나누었을 때 나머지만 count 해 보겠습니다.

65536은 65536으로 나누었을 때 나머지가 0입니다. 65539는 3, 65538은 2입니다. 고로, count 배열에는 위와 같이 들어가게 됩니다.
- 우리는 3번째로 작은 수를 찾아야 합니다.
- 이미 몫이 0인 것의 개수는 1개였습니다.
- 몫이 1인 것 중에는 2번째로 작은 수를 찾아야 합니다.
따라서, 나머지가 2이고, 몫이 1인 65538이 3번째로 작은 수가 됩니다. 이를 바탕으로 구현해 봅시다.
k번째 작은 수 찾기 코드 구현하기
코드 구현은 그리 어렵지 않습니다. -10억보다 크거나 같고, 10억보다 작거나 같은 수들이 n개 있다고 했습니다. 이 경우
- 모든 수에 10억을 더합니다.
- 그러면 모든 수들은 65536a + b꼴로 나타내어 집니다.
k번째 작은 수는 65536으로 나누었을 때 몫이 얼마인지부터 구해 봅시다.
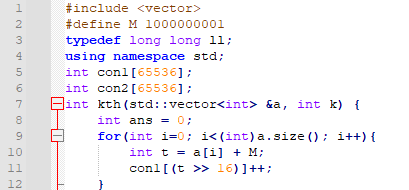
먼저, 65536으로 나눈 몫이 k인 수의 개수를 count 해야 한다고 했습니다. 9번째 줄의 for loop 안을 보면, con[(t >> 16)]++; 이라는 문장을 볼 수 있는데요. 65536으로 나눈 몫을 계산해서, count 배열에 하나 증가시키는 것입니다.
10번째 줄은 배열의 값에 M을 더했는데요. 들어올 수 있는 작은 수가 -10억이기 때문에, 이보다 큰 10억 1을 더해주었습니다.
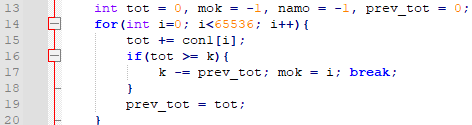
이제, 후보 범위를 구해야 합니다. 몫이 0인 것부터 65535인 것까지 모두 돌면 됩니다. 계속 tot을 누적시키는 것을 볼 수 있는데요. tot의 경우, 몫이 i 이하인 것의 개수를 의미해요. 이 개수가 k보다 크거나 같은 최초의 시점에, 17번째 줄에서 멈추고 빠져나오고 있음을 알 수 있어요.
이제, 몫이 mok인 수에서 k’번째 수를 구하는 것인데요. 이 k’은 k에서 몫이 x보다 작은 수의 개수를 빼면 됩니다. 이는, k -= prev_tot 에서 하고 있습니다.

몫이 구해졌다면, 이제, 나머지만 남았습니다. 배열에 있는 수 중, 몫이 mok인 것만 취해서, 나머지를 카운트 합니다. 24번째 줄의 if문이 이를 수행하고 있습니다. 이 시점에, 몫은 고정입니다. 나머지가 고정이 아니지요. 나머지가 작다면, 수도 작습니다.
28번째 줄의 for loop를 보면, tot는 몫이 mok이고, 나머지가 i 이하인 수의 개수를 의미합니다. 몫은 모두 같습니다. 따라서, tot이 k보다 커지거나 같아지는 시점이 되면, 나머지를 체크하고 빠져나오면 됩니다. 30번째 줄은 이를 수행합니다.
여기서 질문. -1018보다 크거나 같고, 1018보다 작거나 같은 수가 n개 들어옵니다.
- k번째 작은 수를 어떻게 O(n) 만에 찾을까요?
- k번째를 선택하는 것과 k개를 정렬하는 것은 다른 문제입니다. ↩︎